Unlocking the Power of Linear Regression: A Step-by-Step Guide for Beginners

Introduction

Linear regression is a statistical technique that helps us to predict the value of a dependent variable based on the values of one or more independent variables. It is one of the most commonly used techniques in statistical modeling and can be applied to a wide range of fields, from economics to social sciences.

To understand linear regression, let's take an example of predicting the salary of an employee based on their years of experience. In this case, the dependent variable is the salary, and the independent variable is the years of experience.

Steps for Implementing Linear Regression

To create a linear regression model, we first need to collect data on salaries and years of experience. Once we have the data, we can plot it on a scatter plot to see if there is any relationship between the two variables.

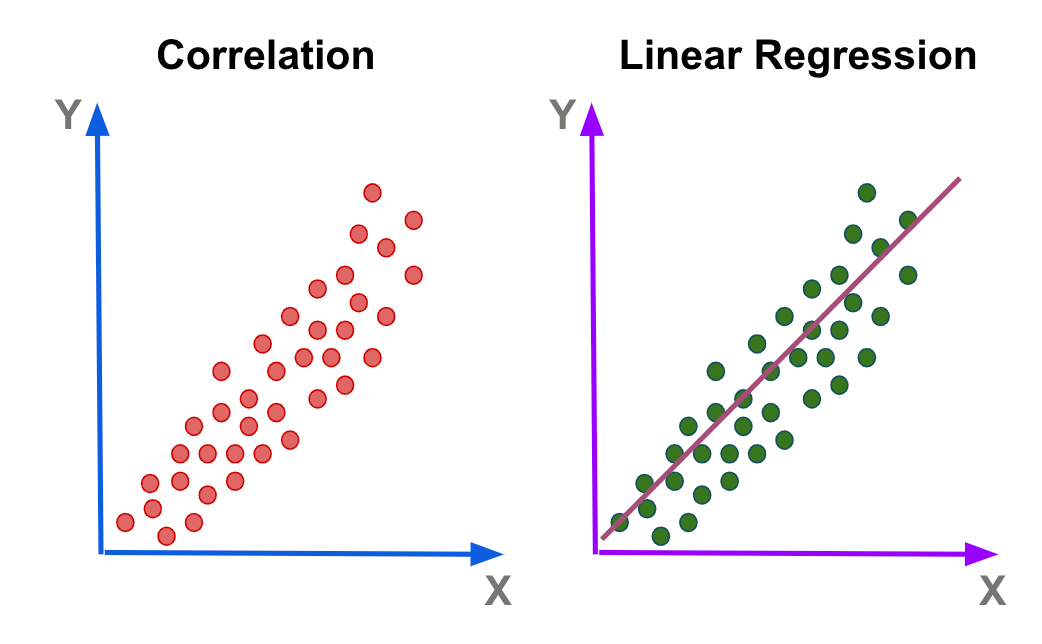
The scatter plot will show us a positive correlation between the two variables, indicating that as the years of experience increase, the salary also tends to increase. To create a linear regression model, we can use the least-squares regression method, which minimizes the sum of the squared errors between the predicted and actual values.

Using this method, we can find the slope and intercept of the line that best fits the data points. The slope represents the rate of change in the dependent variable for every unit increase in the independent variable, while the intercept represents the value of the dependent variable when the independent variable is zero.

Once we have the slope and intercept values, we can use the linear equation to predict the salary of an employee based on their years of experience.

Example of Linear Regression

if the slope is 5000 and the intercept is 30000, the linear equation would be:

salary = 5000 \ years of experience + 30000*

Suppose we want to predict the salary of an employee who has 10 years of experience. We can plug in the value of 10 for years of experience and solve for salary:

salary = 5000 \ 10 + 30000 = 80000*

Therefore, we can predict that the salary of an employee with 10 years of experience would be 80000.

It's essential to note that linear regression assumes a linear relationship between the dependent and independent variables. If the relationship is nonlinear, then linear regression may not be the best technique to use.

Conclusion

Linear regression is a powerful statistical technique that can help us make predictions based on data. By using this technique, we can identify relationships between variables and make informed decisions based on the results.